Algorytmy i struktury danych odgrywają kluczową rolę w informatyce i programowaniu. Ich zrozumienie pozwala tworzyć wydajne i optymalne programy, dlatego warto poświęcić czas na dogłębne poznanie tej tematyki. W niniejszym artykule przyjrzymy się najważniejszym zagadnieniom związanym z algorytmami i strukturami danych, aby krok po kroku zdobyć solidne podstawy w tej dziedzinie.
Podstawy algorytmów
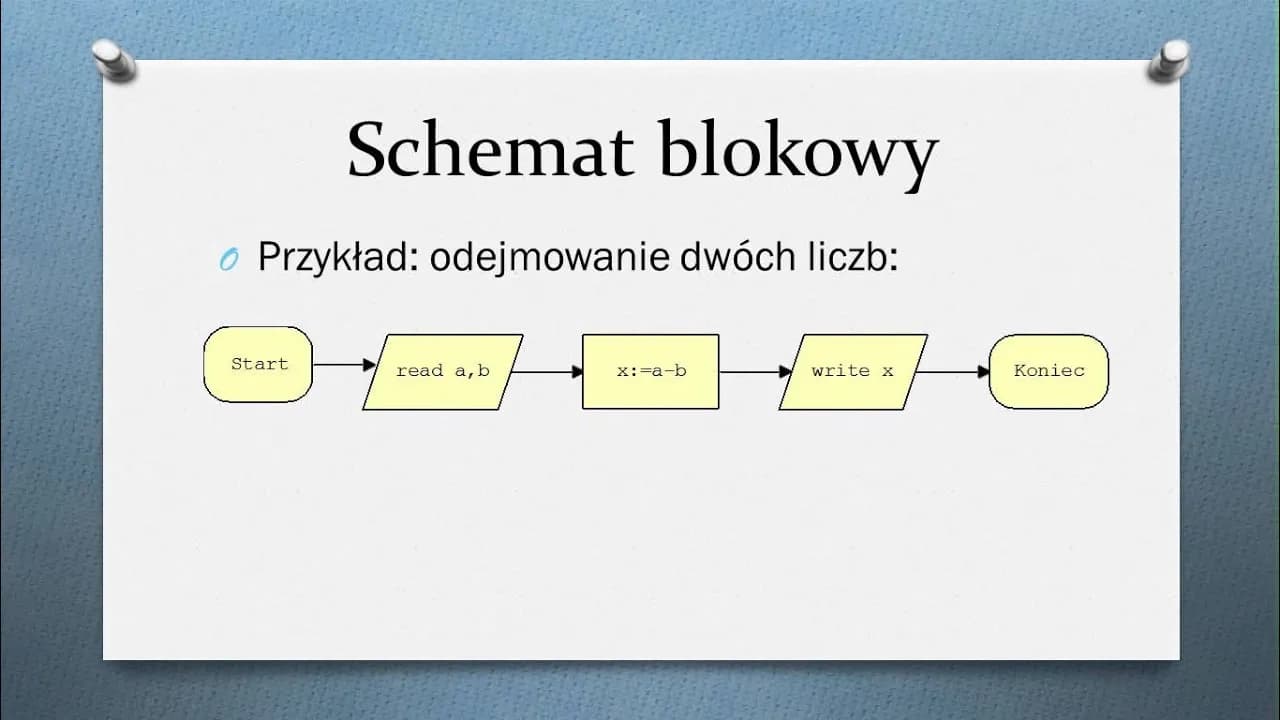
Na początku warto wyjaśnić, czym właściwie jest algorytm. Jest to precyzyjny, skończony zbiór jednoznacznych instrukcji służących do rozwiązania danego problemu lub wykonania określonego zadania. Algorytmy stanowią sekwencję kroków, które należy podjąć, aby transformować dane wejściowe w oczekiwane dane wyjściowe. Ich celem jest uzyskanie poprawnego wyniku w skończonej liczbie kroków. Język, w jakim formułowany jest algorytm, musi być precyzyjny i nie powinien dopuszczać wieloznaczności. Najpopularniejsze sposoby zapisu algorytmów to pseudokod, schemat blokowy oraz języki programowania.
Tworząc algorytmy, dążymy do tego, aby były one poprawne, zrozumiałe i możliwie jak najefektywniejsze. Poprawność oznacza, że algorytm faktycznie prowadzi do otrzymania oczekiwanego rezultatu. Ważna jest również czytelność zapisu, która ułatwia zrozumienie działania algorytmu. Wreszcie kluczowe znaczenie ma efektywność, czyli zdolność algorytmu do znalezienia rozwiązania w jak najkrótszym czasie oraz przy jak najmniejszym zużyciu zasobów, takich jak pamięć.
Struktury danych w algorytmach
Oprócz sposobu działania, istotną kwestią w algorytmach jest struktura danych, na której operują. Struktury danych to sposoby organizacji i przechowywania danych w pamięci komputera. Wybór odpowiedniej struktury ma znaczący wpływ na wydajność algorytmu.
Podstawowymi strukturami danych są tablica i rekord. Tablica pozwala przechowywać elementy o tym samym typie w konkretnej kolejności, natomiast rekord grupuje różne elementy o rozmaitych typach. Bardziej zaawansowane struktury to m.in. stos, kolejka, lista czy drzewo. Każda z nich ma swoje zalety i wady.
Na przykład stos, działający na zasadzie LIFO (last in, first out), sprawdzi się w sytuacjach, gdy priorytet mają ostatnio dodane elementy. Z kolei kolejka FIFO (first in, first out) przyda się, gdy istotna jest kolejność dodawania elementów. Wybierając odpowiednią strukturę danych, możemy znacząco zoptymalizować działanie algorytmów.
Czytaj więcej: Analiza złożoności algorytmów w pigułce - notacje O(n), theta, omega
Algorytmy sortowania
Sortowanie bąbelkowe
Jedną z podstawowych funkcjonalności w informatyce jest sortowanie, czyli układanie elementów według pewnego porządku – najczęściej rosnącego lub malejącego. Klasycznym przykładem jest tu sortowanie bąbelkowe. Polega ono na wielokrotnym przechodzeniu przez tablicę i porównywaniu sąsiednich elementów. Jeśli są nieprawidłowo ułożone, zamieniane są miejscami. Operacja powtarzana jest aż do momentu, gdy przejdziemy przez tablicę bez żadnych zamian.
Sortowanie przez wstawianie
Innym prostym algorytmem sortowania jest sortowanie przez wstawianie. Zaczynamy od założenia, że element pierwszy jest uporządkowany. Następnie bierzemy kolejne elementy i wstawiamy je we właściwe miejsce w dotychczas posortowanej części tablicy, przesuwając elementy w prawo, jeśli trzeba. Operacja jest powtarzana dla wszystkich elementów.
Sortowanie przez wybieranie
Jeszcze innym klasycznym algorytmem jest sortowanie przez wybieranie. W tym przypadku z tablicy wybierany jest najmniejszy element i umieszczany na pierwszej pozycji. Następnie wybieramy najmniejszy element z pozostałej części tablicy i kładziemy go na drugim miejscu itd. Operacja powtarzana jest aż do wyczerpania wszystkich elementów.
Algorytmy wyszukiwania
Wyszukiwanie liniowe
Częstym zadaniem w informatyce jest wyszukiwanie konkretnego elementu w zbiorze danych. Najprostszym rozwiązaniem jest wyszukiwanie liniowe, czyli sprawdzenie kolejno każdego elementu tablicy, aż znajdziemy poszukiwany obiekt lub dojdziemy do końca tablicy. Jest ono bardzo proste do implementacji, ale ma liniową złożoność obliczeniową.
Wyszukiwanie binarne
Znacznie szybsze od wyszukiwania liniowego jest wyszukiwanie binarne. Jednak w tym przypadku tablica musi być uprzednio posortowana. Polega ono na wyznaczeniu środkowego elementu w tablicy, sprawdzeniu go i na tej podstawie zawężeniu przedziału poszukiwań do lewej lub prawej połowy tablicy. Operacja powtarzana jest aż do znalezienia elementu.
Drzewa binarne
Jeszcze inną metodą organizacji danych ułatwiającą wyszukiwanie są drzewa binarne. Elementy są w nich uporządkowane hierarchicznie, tworząc strukturę przypominającą odwrócone drzewo. Umożliwia to bardzo szybkie przeszukiwanie, zazwyczaj logarytmicznej złożoności.
Algorytmy zachłanne
Problem plecakowy
Algorytmy zachłanne bazują na podejmowaniu lokalnie optymalnych wyborów w nadziei, że doprowadzi to do globalnie optymalnego rozwiązania. Typowym przykładem jest tu problem plecakowy, w którym chcemy spakować jak najcenniejsze przedmioty do plecaka o ograniczonej pojemności. Algorytm zachłanny będzie brał najpierw najcenniejsze przedmioty, aż do wyczerpania miejsca.
Problem wydawania reszty
Podobnie działa zachłanny algorytm rozwiązujący problem wydawania reszty przy użyciu jak najmniejszej liczby monet. Na początku weźmie największą dostępną monetę mniejszą od kwoty reszty, potem następną itd. Dzięki temu uzyska optymalny wynik.
Problem komiwojażera
Klasycznym problemem, w którym stosuje się algorytm zachłanny, jest problem komiwojażera znajdującego najkrótszą trasę przechodzącą przez szereg miast. Algorytm na początku wybiera najbliższe miasto i kontynuuje w ten sposób aż do odwiedzenia wszystkich.

Złożoność algorytmów
Złożoność czasowa
Porównując różne algorytmy, bardzo ważne jest oszacowanie ich złożoności czasowej, czyli ilości operacji jakie muszą wykonać w zależności od rozmiaru danych wejściowych. Pozwala to ocenić, jak będą się skalować przy rosnącej ilości danych.
Złożoność pamięciowa
Oprócz złożoności czasowej, istotna jest również złożoność pamięciowa, czyli zapotrzebowanie algorytmu na pamięć operacyjną. Algorytmy o dużym „apetycie” na pamięć mogą okazać się niepraktyczne przy ogromnych zbiorach danych.
Notacja dużego O
Do wyrażania złożoności algorytmów stosuje się zazwyczaj notację dużego O, która pozwala zasygnalizować rząd wielkości złożoności w uproszczony sposób. Na przykład O(n) dla algorytmów liniowych czy O(log n) dla algorytmów logarytmicznych.
Jak widać, algorytmy i struktury danych stanowią rozległą i złożoną dziedzinę wiedzy, lecz opanowanie choćby jej podstaw pozwoli znacząco zwiększyć umiejętności programistyczne. Kluczem jest stopniowe zgłębianie poszczególnych zagadnień - wtedy nawet ta skomplikowana tematyka staje się jasna i przystępna.
Podsumowanie
Algorytmy i struktury danych stanowią fundament zaawansowanego programowania. Ich dokładne zrozumienie pozwala tworzyć oprogramowanie nie tylko poprawne, ale przede wszystkim wydajne. Najważniejsze jest stopniowe poznawanie kolejnych zagadnień - od podstawowych algorytmów, przez struktury danych, aż po bardziej złożone techniki. Systematyczna nauka, dużo praktyki i cierpliwości z pewnością pozwolą opanować tę kompleksową dziedzinę wiedzy.